Croissance strictement exponentielle 

La croissance strictement exponentielle n’existe pas dans la nature, mais son étude, au moins comme contre-exemple, est très instructive.

Nous imaginerons un réseau plan à croissance centrale strictement exponentielle et parfaitement régulière.

Le plan sera rapporté à un repère (O, i, j) orthonormé.

La “cellule” de rang n sera représentée par un disque de centre M_n (x_n , y_n ), et de rayon égal à r_n.

Nous supposerons, pour simplifier les calculs, que  OM₀ = 1.

On passe d’une “cellule” à la suivante par une similitude (ou homothétie complexe) de rapport k (réel) et d’angle , ce qui se traduit par les égalités :

Ø     r_n = kⁿ . r₀

Ø     x_n = kⁿ . cos(n . )

Ø     y_n = kⁿ . sin(n . )

Trois constantes interviennent :

Ø     r₀, rayon du disque initial ;

Ø     k, rapport de la similitude;

Ø     , angle de la similitude.

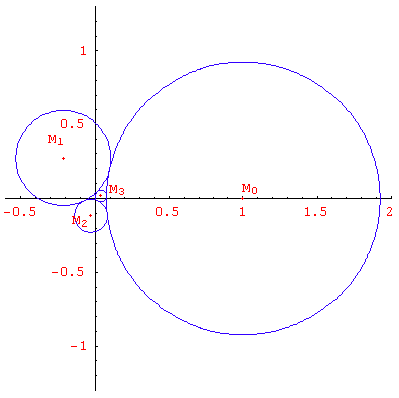
Notre but est de choisir ces trois constantes, de telle sorte que chaque disque soit tangent aux trois précédents et aux trois suivants.

En pratique, il suffit de s’assurer que le disque initial (de rang 0) soit tangent aux trois suivants (de rangs 1, 2, 3) : ce qui est vrai pour l’un des disques l’est aussi pour tous les autres.

On doit donc avoir :

M₀ M₁ = r_{0 +} r_{1 ,}  M₀ M₂ = r_{0 +} r_{2 ,}  M₀ M₃ = r_{0 +} r₃ , ce qui entraîne :

Ø     (k.cos –1)² + (k.sin –1)² = (r₀ + k. r₀)²

Ø     (k².cos (2 ) –1)² + (k².sin (2 ) –1)² = (r₀ + k². r₀)²

Ø     (k³.cos (3 ) –1)² + (k³.sin (3 ) –1)² = (r₀ + k³. r₀)²

Pour simplifier l’écriture, posons :  c = cos   et  r = r₀.

On a alors :  cos (2 ) = 2 c² – 1   et   cos (3 ) = 4 c³ – 3 c.

Les égalités précédentes deviennent :

Ø     k² – 2 k c + 1 = r² (1 + k)²

Ø     k⁴ – 2 k² (2 c² – 1) + 1 = r² (1 + k²)²

Ø     k⁶ – 2 k³ (4 c³ – 3 c) + 1 = r² (1 + k³)².

On en tire :

Les égalités (1) deviennent :

Pour r 0 (soit X – 2 c 0), on peut en tirer :

(X + 2 c).(X + 2) = X²   et   X² + 2 c X + 4 c² – 3 = X² - 2 X + 1.

Ces équations se ramènent au premier degré. On en tire :

Ce qui entraîne :  c = (c + 1).(c – 1) = c² – 1,  donc :  c² = c + 1.

Nous reconnaissons l’équation bien connue qui a pour solutions :  c =   et  c = .

Nous éliminons la première solution (supérieure à 1) et conservons la seconde :

Ces deux nombres sont inverses ; ils correspondent à la même structure, mais avec inversion de la numérotation des cellules.

Notre problème possède donc une solution non triviale unique (au sens près).

Cette solution fait intervenir le nombre d’or, et pourtant la divergence qui en résulte (128° 10’) n’est pas égale à la section d’or (137° 30’).

Dans cette croissance exponentielle, les contacts entre les cellules sont figés : il n’y a pas de changements de maille. La structure n’évolue pas, et la divergence reste bloquée à sa valeur initiale, qui n’est pas égale à la section d’or.

Tout l’intérêt de cet exemple imaginaire est de montrer que la clé des maillages de Fibonacci n’est pas dans les conditions initiales, mais dans le travail algorithmique des mailles, qui force la divergence à évoluer vers la section d’or.

Dans le domaine de la botanique, la croissance n’est pas exponentielle : elle est toujours plus lente, et c’est précisément ce qui permet les changements de maille, rendus obligatoires par les contraintes géométriques.

Observons la figure ci-dessus : on conçoit facilement que la croissance centrale ne va pas permettre aux cellules initiales (0, 1, 2) de conserver leurs contacts réciproques : ils vont nécessairement céder, mais dans quel ordre ? Si le choix s’effectue, à chaque étape, selon le même critère, alors la structure va évoluer de manière algorithmique.