La suite de Farey

A deux fractions quelconques, on peut associer leur fraction médiane, obtenue en additionnant les numérateurs entre eux et les dénominateurs entre eux :

Pour construire la suite de Farey, nous partons de la séquence initiale :

puis, entre ces deux fractions, nous plaçons leur fraction médiane, ce qui donne :

De nouveau, nous intercalons, entre deux fractions successives, leur fraction médiane. Nous obtenons les séquences suivantes :

Et ainsi de suite.

Ces séquences possèdent des propriétés remarquables :

·        dans chaque séquence, deux fractions successives (c/a et d/b) vérifient toujours l’égalité :    a.d – b.c = 1 ;

·        les nombres a et b sont premiers entre eux, de même que c et d, a et c, b et d ;

·        toutes les fractions obtenues sont irréductibles ;

·        elles sont rangées dans l’ordre croissant ;

·        si on continue indéfiniment, chaque nombre rationnel compris entre 0 et 1 apparaît une fois et une seule ;

·        si deux fractions c/a et d/b, comprises entre 0 et 1, vérifient l’égalité : a.d – b.c = 1, alors ce sont deux fractions successives dans l’une des séquences de Farey ;

·        parmi les fractions comprises entre c/a et d/b (où : a.d – b.c = 1), une seule a un  dénominateur égal à a+b : c’est la fraction médiane ; toutes les autres ont un dénominateur supérieur à a+b.

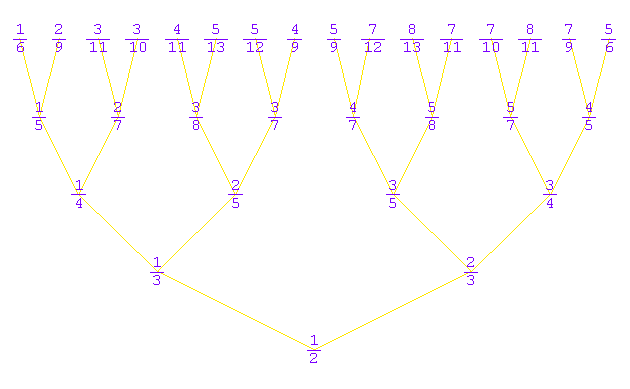
La suite de Farey peut être représentée par un arbre (appelé : arbre de Stern-Brocot) :

De bas en haut, ligne par ligne, nous trouvons les fractions dans leur ordre d’apparition.

Dans cet arbre, chaque nombre rationnel compris entre 0 et 1 a une place bien définie, qui peut être codée par une suite finie de symboles (par exemple : G pour gauche et D pour droite).

Rappelons que dans les systèmes de numération usuels (décimal ou binaire par exemple), qui sont basés sur les suites géométriques, une infinité de nombres rationnels sont codés par des suites illimitées ; ici, seuls les nombres irrationnels sont codés par des suites illimitées.

La suite illimitée alternée : GDGDGDGD….  est associée au nombre :

et la suite :   DGDGDGDG….  est associée à :

Ces deux nombres correspondent (au sens près) à la même divergence : c’est la section d’or (exprimée en tours).

Le premier est la limite de la suite :

et le second est la limite de :

Ces fractions de Fibonacci sont faciles à repérer dans les séquences de Farey : ce sont celles qui ont le plus grand dénominateur.

La suite de Farey fournit une méthode très générale pour calculer des encadrements rationnels de nombres réels quelconques.

On peut l'utiliser par exemple dans l'étude du calendrier (encadrements des quotients : jour/année solaire, ou mois lunaire/année solaire), de la musique (encadrements du quotient quinte/octave), et surtout des parastiques (encadrements de la divergence).

La divergence (div) étant donnée (nombre réel compris entre 0 et 1), on calcule des encadrements rationnels de plus en plus fins, en remplaçant, à chaque étape, l'une des deux bornes par la médiane des deux bornes. Ces bornes sont deux fractions dont les dénominateurs indiquent les nombres de parastiques.

Considérons, par exemple, l’encadrement suivant  (1) :

et cherchons un encadrement plus fin ; pour cela, il faut faire intervenir une fraction comprise entre c/a et d/b ; si nous voulons qu’elle ait le plus petit dénominateur possible, il faut prendre la fraction médiane. La question qui se pose alors est de savoir si cette fraction médiane est supérieure, égale ou inférieure à la divergence ; selon le cas,on aura :

Quand nous parcourons l’hélice génératrice, pour a entrenœuds, nous faisons à peu près c tours (un peu plus), et pour b entrenœuds, à peu près d tours (un peu moins). Le couple (a, b) correspond à une combinaison des parastiques, qui s’actualise pour un entrenœud compris dans une certaine fourchette. Si nous réduisons l’entrenœud, à partir d’un seuil (calculable), la fraction médiane va entrer en jeu ; la nouvelle combinaison de parastiques sera alors soit (a, a+b), si la fraction médiane est supérieure à la divergence, soit (a+b, b), dans le cas contraire.

Connaissant la divergence, cet algorithme (facile à programmer) permet de calculer la séquence d’actualisation des parastiques, en partant de l’encadrement initial :

Inversement, pour une combinaison donnée (a, b) de parastiques actuelles (avec a et b premiers entre eux), on peut donner un encadrement de la divergence : il suffit de trouver les nombres c et d permettant de reconstituer l’encadrement (1) ci-dessus, donc vérifiant l’égalité : a.d – b.c = 1, avec :  0 < c < d < b.

Autrement dit : on cherche le plus petit entier naturel n tel que 1+b.n soit divisible par a, ce qui nous donne la valeur de c, puis on calcule d = (1+b.c)/a.

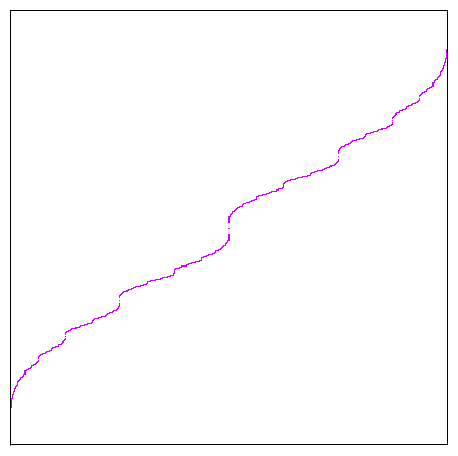
Une autre façon de visualiser la suite de Farey consiste à tracer, point par point, la courbe ci-dessous.

Pour cela, on part des points initiaux (0/1 ; 0/1) et (1/1 ; 1/1), puis on place leur point médian (1/2 ; 1/2), ensuite (1/4 ; 1/3) et (3/4 ; 2/3), etc. : entre deux points successifs, on place leur “point médian”, obtenu en calculant la moyenne arithmétique des abscisses et la médiane des ordonnées.

Définie d’abord pour les rationnels, cette fonction peut être prolongée par continuité pour tous les nombres réels compris entre 0 et 1.

C’est une fonction strictement croissante, continue partout mais dérivable nulle part.

              RETOUR