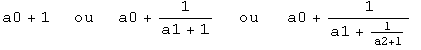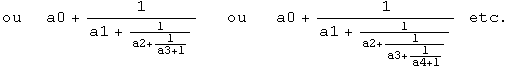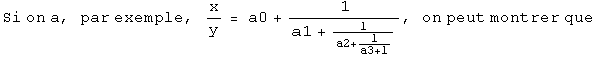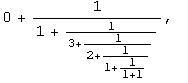Suite de Farey et fractions continues

Cette page présente quelques outils mathématiques très généraux qu’ on est amené à utiliser quand on étudie les hélices régulières de divergence quelconque .

Considérons 1' ensemble E des points du plan à coordonnées entières premières entre elles.

Les points situés dans le premier quadrant illustrent 1' ensemble des nombres rationnels positifs : toute fraction irréductible x/y est représentée par un point de coordonnées (x, y).

Cette représentation des nombres rationnels comme points discrets du plan (et non alignés sur une droite) est, de beaucoup, la plus instructive pour les problèmes qui nous occupent. (On pourrait également associer, à chaque nombre réel, une droite passant par l’ origine.)

Dans ce contexte, le calcul de la médiane de deux fractions se ramène à une somme vectorielle.

Une étude intéressante à mener serait 1' étude exhaustive des transformations linéaires qui laissent 1' ensemble E globalement invariant, ou encore des matrices 2 x 2 à coefficients entiers relatifs et à déterminant égal à  + 1 ou à  - 1.

Cet ensemble de matrices, muni de la multiplication matricielle, est un groupe non commutatif. On l'appelle "groupe spécial linéaire unitaire" ; le sous-groupe à déterminant égal à 1 est connu sous le nom de SL(2, Z) : c'est le "groupe spécial linéaire de deuxième ordre sur les nombres entiers", ou "groupe modulaire homogène". Quant au vrai groupe modulaire ( le "groupe modulaire inhomogène", ou "groupe modulaire homographique"), il est isomorphe à SL(2, Z)/{I, -I}. Nous reviendrons sur le groupe modulaire homogène sur une autre page.

Posons :

On peut vérifier facilement les égalités suivantes :

(Pour ces deux dernières égalité voir le paragraphe sur la suite de Fibonacci) .

Les valeurs propres de D et G sont 0 et 1. Celles de A et B sont et .

Revenons maintenant à la suite de Farey : nous avons expliqué comment on peut coder la position d ' une fraction irréductible (comprise entre 0 et 1) dans 1'arbre de Stern - Brocot, à l' aide de deux symboles (par exemple G pour gauche et D pour droite).

Il est facile de généraliser ce codage à 1' ensemble nombres rationnels strictement positifs : il suffit de partir des fractions 0/1 et 1/0 .

Prenons par exemple la fraction 27/35 : selon ce principe, elle se code sous la forme GDDDGGDG (G pour gauche et D pour droite).

Or on peut vérifier que 1' on a :

Ceci se généralise : le repérage d'un nombre rationnel dans l'arbre de Stern - Brocot équivaut à la recherche d' une combinaison de matrices de type G et D.

Venons - en maintenant aux fractions continues.

On sait que tout nombre rationnel strictement positif peut s ' écrire sous 1 ' une des formes suivantes (où a0, a1, a2, etc., sont des nombres entiers naturels):

(Le terme +1 qui apparaît en bas à droite est destiné à assurer 1' unicité de la décomposition) .

A chaque rationnel strictement positif correspond, de manière biunivoque, une suite finie d' entiers (a0, al, a2, a3, ...) tous différents de 0, sauf éventuellement le premier (a0) .

La construction de ces fractions superposées peut s' interpréter à 1' aide de matrices.

Pour cela, remarquons tout d' abord que 1' application qui, à tout rationnel r = x/y, associe n + 1/r = n + 1/(x/y) = n + y/x = (n.x + y)/y, ou, si on préfère, qui, à tout vecteur (x, y), associe le vecteur (n.x + y, x), a pour matrice :

Ceci, également, se généralise : la décomposition d'un nombre rationnel en fraction continue équivaut à la recherche d' un produit de matrices de type An .

Reprenons 1' exemple de la fraction 27/35 : elle est égale à

et la suite correspondante est donc (0, 1, 3, 2, 1, 1), ce qui peut s' écrire de manière matricielle : A₀. A₁. A₃. A₂. A₁. A₁ , ou encore, compte tenu des égalités vues plus haut :

soit, après simplification :

ce qui correspond à la décomposition selon 1' arbre de Stern-Brocot.

En définitive, les coefficients de la décomposition en fraction continue sont les exposants de la décomposition selon l'arbre de Stern - Brocot.

(Attention cependant au premier coefficient, qui est 0 dans notre exemple : il correspond à un facteur D⁰ qu ' on pourrait faire figurer au début de la décomposition selon 1' arbre de Stern - Brocot : cette décomposition doit commencer par D et non par G, pour que les matrices J s' éliminent correctement.)

On sait que le PGCD de deux nombres entiers naturels x et y se calcule usuellement par deux méthodes : la “méthode des soustractions” et la “méthode des divisions” (ou algorithme d’ Euclide). La première se rattache très étroitement à la décomposition du nombre x/y selon l’arbre de Stern-Brocot, et la seconde à sa décomposition selon le principe des fractions continues.

Voici un programme en Java Script permettant de passer d' un code à l' autre :

Codage des nombres rationnels

Donnez l'écriture d'un nombre rationnel (strictement positif) dans l'un des trois codes suivants (au choix), et le programme le traduira dans les deux autres codes :

 Voici un nouveau programme, destiné à montrer comment les transformations de matrices D et G (et leurs inverses) agissent sur l’ensemble E des points à coordonnées premières entre elles. (Ces points sont représentés en vert sur la figure.)

Pour voir cette animation, cliquez ici.

Un point quelconque à coordonnées positives, entières et premières entre elles (xi, yi) peut être amené en (1, 1) par une combinaison finie de transformations de type G- et D-. Inversement, si on part du point (1, 1) et si on le transforme à l’ aide des matrices G et D, il va balayer l’ ensemble des points à coordonnées premières entre elles situés dans le premier quadrant. A chacun de ces points (xi, yi) correspond une combinaison unique de ces matrices G et D : c’est la décomposition du nombre rationnel xi/yi selon l’ arbre de Stern-Brocot.

Si on veut travailler sur l’ ensemble E tout entier (sans se limiter au premier quadrant), le problème est un peu plus complexe : il faut faire entrer en jeu les quatre matrices (D+, D-, G+, G-) ; l’ unicité des décompositions n’ est plus assurée.

Une base (i, j) telle que  i = (xi, yi) et j = (xj, yj), où xi, yi, xj et yj sont quatre entiers relatifs vérifiant l’ égalité : xi.yj – xj.yi = 1, peut être transformée en i = (1, 0) et j = (0, 1) par une succession des mêmes transformations (D+, D-, G+, G-).

On s’ en convaincra aisément grâce au jeu suivant :

On part de deux vecteurs : i = (xi, yi) et j = (xj, yj), vérifiant : xi.yj - xj.yi = 1, et on transforme la base (i, j) en utilisant seulement matrices D+ et G+, et leurs inverses D- et G-.

La matrice D+ transforme j en j + i ; la matrice D- transforme j en j – i ; la matrice G+ transforme i en i + j ; la matrice G- transforme i en i - j.

Il faut d'abord choisir les nombres entiers xi et yi, premiers entre eux. Les nombres xj et yj (qui sont définis modulo (xi, yi)) sont ensuite calculés automatiquement.
Le but est d'aboutir à i = (1, 0) et j = (0, 1).

Si xi et yi sont positifs, on obtiendra ce résultat en utilisant seulement D- et G-.
Autrement dit, si on transforme la base (i = (1, 0) ; j = (0, 1)) à l’ aide des matrices G et D seulement, on pourra obtenir toutes les bases (i = (xi, yi) ; j = (xj, yj)) à coefficients entiers naturels tels que : xi.yj - xj.yi = 1.

Encore une question qui peut amuser les mathématiciens : savez-vous quelle est la densité de l’ ensemble E ? Autrement dit : deux nombres entiers étant choisis de manière aléatoire, quelle est la probabilité pour qu’ ils soient premiers entre eux ?

Nous ne traiterons pas ce sujet de façon rigoureuse, mais nous indiquerons brièvement trois idées :

Ø     Observons (voir ci-dessus) la figure représentant l’ ensemble E, et exploitons ses symétries. Isolons un triangle ayant pour sommets les points de coordonnées (0, 0), (n, 0) et (n, n). L’ aire de ce triangle est égale à n²/2. Comptons les points de E situés dans ce triangle, colonne par colonne. Le nombre de points d’ abscisse i (2  i  n) est égal à (i), c’ est-à-dire au nombre d’ entiers inférieurs à i et premiers avec lui. (Nous désignons par  la fonction phi d' Euler.) Si nous appelons x la densité de E, nous pouvons écrire

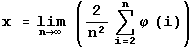
Ø     Appelons E1 l’ ensemble des couples d’ entiers dont le PGCD est 1 (donc E1 = E), E2 l’ ensemble des couples dont le PGCD est 2, etc. E2 se déduit de E1 par une homothétie de rapport 2 ; sa densité est donc x/4. De même, la densité de E3 est x/9, celle de E4 est x/16, etc. Comme chaque couple d’ entiers appartient à un, et un seul, de ces ensembles, on en déduit :

Nous notons  la fonction zéta de Riemann. On sait que : 

Donc :    x = 6/ ² =  0,6079…

Ø     Raisonnons maintenant en termes de probabilités. Considérons un couple d’ entiers choisis aléatoirement. Ils seront premiers entre eux s’ ils n’ ont aucun diviseur premier en commun. La probabilité pour qu’ ils ne soient pas tous les deux divisibles par 2 est : 1 – 1/2² , la probabilité pour qu’ ils ne soient pas tous les deux divisibles par 3 est : 1 – 1/3² , etc. D’ où l’ égalité :

où  (i) désigne le i^ème nombre premier (et non le nombre ).

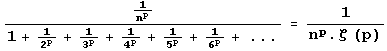
Mais ici nous nous éloignons beaucoup de la stricte étude des hélices régulières ...

                   RETOUR